Поделиться:

Олимпиада по математике 9 класс.

1. Как посадить 10 яблоней, чтобы нашлось 5 рядов, в каждом из которых ровно 4 яблони?
2. В параллелограмме ABCD стороны AB и BC равны 4 и 7 соответственно. Биссектрисы AK и BM углов параллелограмма пересекаются в точке O (точки K и M лежат на сторонах BC и AD соответственно). Во сколько раз площадь пятиугольника OKCDM больше площади треугольника OAB?
3. В противоположных углах квадратной комнаты положили два одинаковых ковра. Площадь их общей части оказалась равна 50дм2. Затем один из ковров развернули в углу на 90°. Площадь общей части стала равна 25дм2. На сколько длина ковра больше его ширины?

4. Докажите, что в десятичной записи числа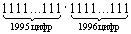     

 найдется цифра, которая встретится не менее400 раз.

5. Однажды несколько друзей обменивались рукопожатиями. В некоторый момент оказалось, что среди любых четырех из них имеется хотя бы один человек, который успел пожать руки трем другим. Доказать, что друзьям осталось сделать не более трех рукопожатий.

 

Олимпиада по математике   9класс
I этап

1.Найти корни многочлена :         2х ⁵ + х⁴ – 10х³ – 5х² + 8х + 4     (2б.)

2. Решите уравнение :                   х² – 2х - 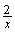 +  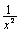- 13 = 0             (3б.)

3. Не решая уравнения   9х² + 18х – 8=0,   найдите  сумму кубов его корней.   (4б.)

4. В юности  М. В. Лермонтов тратил одну денежку на хлеб и квас.  Когда цены
выросли на 20%, на ту же денежку он приобретал полхлеба и квас.
Хватит ли той же денежки хотя бы на квас, если цены ещё раз
вырастут на 20.%?  
(4б.)
5. Окружность, касающаяся гипотенузы  прямоугольного треугольника, а также
продолжений его обоих катетов, имеет радиус 25 см..
Найдите периметр треугольника.                                 (5б.)

6. Двое рабочих могут напилить за день 5 полениц дров, а наколоть 8 полениц.
Сколько полениц дров они должны напилить, чтобы успеть наколоть их
в тот же день?             (5б.)

 

 

ШКОЛЬНАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ

9 класс
1. Постройте эскиз графика функции: .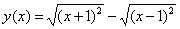
Решение.
Нетрудно понять, что после извлечения корня 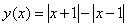. График данной функции является ломаной, и состоит из луча, отрезка и луча. Для каждого из них нужно знать координаты двух точек на плоскости. Составим таблицу: 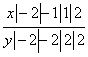. По точкам графика ломаной восстановим ее график:

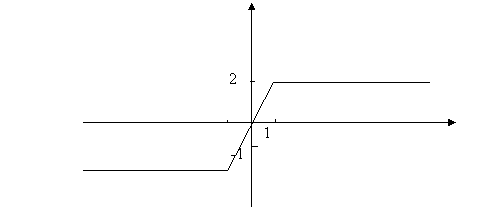
Заметим, что график данной функции традиционно строится и методом интервалов.
2. При каких значениях параметра а уравнение 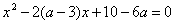 имеет корни одного знака?
Ответ: .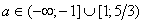
Решение. По теореме Виета произведение корней приведенного квадратного уравнения, если его дискриминант неотрицателен, равно 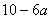. Поэтому имеем систему условий: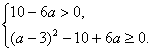
Тогда: 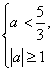. Отсюда .

 

 

 

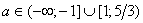3.В прямоугольном треугольнике с катетами 3 и 4 см проведены высота прямого угла и медиана большего из острых углов. В каком отношении высота делит медиану?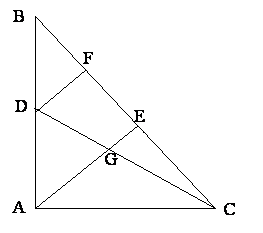
Ответ: 9:8, считая от основания.
Решение. Проведем отрезок DF, параллельный высоте АЕ. По теореме Фалеса, он разделит отрезок BE пополам. По теореме Пифагора, гипотенуза треугольника АВС равна 5 см. Кроме этого 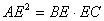, и 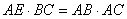. Отсюда: 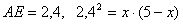. Отсюда 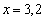. То есть ВЕ=3,2, FE=1,6, EC=1,8. Из параллельности отрезков DF и GE следует, что .
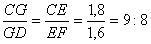4. В пруд пустили 30 щук, которые постепенно поедали друг друга. Щука считается сытой, если она съедает трех щук (сытых или голодных). Каково наибольшее количество щук в этом пруду, которые могли бы почувствовать себя сытыми за достаточно большой промежуток времени?( щука может быть в некоторый момент сытой, но потом съеденной)
Ответ. 9 щук.
Решение. 10 сытых щук быть не может, так как каждая из них съест хотя бы по три щуки и еще последняя останется живой. То есть щук было хотя бы 31. Пример на 9 щук строится просто: первая съела три других, следующая съела ее и две других, и т. д.

5. Пусть х и у – такие целые числа, что 3х+7у делится на 19. Докажите, что 43х+75y тоже делится на 19.
Доказательство. Попробуем представить 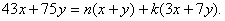 Отсюда:

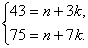 Отсюда, 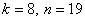. Все