|
 ГДЗ за 1-11 класc ГДЗ за 1-11 класc
|
|
Объявления
На нашем сайте Вы сможете бесплатно скачать задания по егэ и гиа
|
Олимпиада по математике. 8класс.
1. Как посадить 10 яблоней, чтобы нашлось 5 рядов, в каждом из которых ровно 4 яблони?
2. В четырехугольнике ABCD продолжения противоположных сторон AB и CD пересекаются под углом 20°; продолжения противоположных сторон BC и AD также пересекаются под углом 20°. Докажите, что два угла четырехугольника равны, а два других различаются на 40°.
3. Каждую сторону прямоугольника увеличили на 3 см, в результате чего его площадь увеличилась на 39 см2. Найдите периметр исходного прямоугольника.
4. В десятичной записи трех различных чисел используются только цифры 0 и 1.
Может ли одно из этих чисел быть средним арифметическим двух других?
5. Однажды несколько друзей обменивались рукопожатиями. В некоторый момент оказалось, что среди любых четырех из них имеется хотя бы один человек, который успел пожать руки трем другим. Доказать, что друзьям осталось сделать не более трех рукопожатий.
Олимпиада по математике 8класс
I этап
1.Построить график функции y=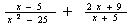 (2б.) (2б.)
2. В выражении 1 – 2 – 4 – 8 –16 = 19 расставьте несколько знаков модуля так,
чтобы равенство стало верным. (3б.)
3. Пусть AC-наибольшая сторона треугольника ABC. На стороне AC выбраны
точки N и M такие, что AM=AB, CN=CB.
Докажите, что если BM=BN, то треугольник ABC равнобедренный.(4б.)
4. Четырёх кошек взвесили попарно во всех возможных комбинациях.
Получились массы : 7 кг; 8 кг; 9 кг; 10 кг; 11 кг; 12 кг.
Какова общая масса всех кошек? (5б.)
5. У Пети есть торт квадратной формы, в трёх углах (в верхних и правом нижнем)
и в самом центре которого находится по изюминке. Петя хочет двумя прямыми
разрезами разделить торт на 4 части, каждая из которых будет с изюминкой, так, чтобы ему достался кусок с изюминкой в правом верхнем углу и он составлял 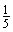 часть торта. Как Петя может разрезать торт? (5б.) часть торта. Как Петя может разрезать торт? (5б.)
Школьная олимпиада по математике
1. Решить систему уравнений. (4б)
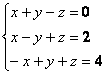
2. Навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист прибыл в В через 2ч после встречи с велосипедистом, а велосипедист прибыл в А через 4,5ч после встречи. Сколько часов в пути был каждый? (6б)
3. Решить в целых числах:
х2—3ху+2у2=3. (4б)
4. Упростить выражение:
(
4x-4- x-2+ 6x-1 -9 ):( 2x-4 + x-3 - 3x-2) (4б)
5. Мальчики составляют 45% всех учащихся в школе. Известно, что 30% всех мальчиков и 40% всех девочек учатся без троек. Сколько % всех учащихся учатся без троек? (4б)
6. Вычислить:
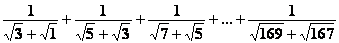 (5б) (5б)
7. Доказать, что сумма трех последовательных степеней числа 2 делится на (3б)
8. Вычислить:
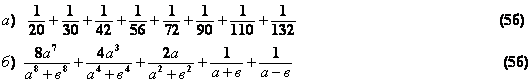
9. Какой цифрой оканчивается сумма 5435+28 21 (4б)
10. Сумма цифр двузначного числа равна 6. Если к этому числу прибавить 18, то получится число, записанное теми же цифрами. Но в обратном порядке. Найдите это число. (5б)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2010/2011 учебный год.
8 класс.
- Рядовой Степанов почистил ведро картошки за 4 часа, однако у него 20% всей картошки ушло в очистки. За сколько часов он наполнит такое же ведро чищеной картошки? (3 балла)
- Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама за 2, сын за 5, бабушка за 10. У них один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если по мосту идут двое, то они идут с меньшей из их скоростей. Идти по мосту без фонарика нельзя. (Светить издали нельзя, перебрасывать фонарик через реку тоже нельзя). (4 балла)
- Решите уравнение: |x - 2005| +|2005 - x | =2006. (4 балла)
- Сколько среди натуральных чисел от 1 до 1983 таких, которые
а) делятся на 7 и на 9;
б) делятся на 9, но не делятся на 7? (4балла)
-
Один из углов треугольника на 1200 больше другого. Докажите, что биссектриса треугольника, проведенная из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины? (5 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2009/2010 учебный год.
8 класс.
- Найдите наименьше число, которое делится на 77, а при делении на 74 дает в остатке 48. (4 балла)
- Отец с двумя сыновьями отправились навестить бабушку, которая живёт в 33км от города. У отца есть мотороллер, скорость которого 25км/ч, а с пассажиром - 20 км/ч (двух пассажиров на мотороллере перевозить нельзя). Каждый из братьев идёт по дороге со скоростью 5 км/ч. Как им надо действовать, чтобы через три часа всей компанией оказаться у бабушки? (6 баллов)
- Один сплав состоит из двух металлов, входящих в него в отношении 2:3. Из скольких частей обоих сплавов можно получить новый сплав, содержащий те же металлы в отношении 17:27? (4 балла)
- Пусть в треугольнике АВС выполняется неравенство АС больше ВС. Докажите, что eсли CD - медиана треугольника АВС, то выполняется условие: угол ACD меньше угла BCD. (5 баллов)
- На огороженном квадратном поле, сторона которого равна 1км, были построены заборы, разделившие его на прямоугольные участки, размеры которых 5м на 20м и 6м на 12м. Какова общая длина построенных заборов? (6 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2008/2009 учебный год.
8 класс.
- Клетки доски 8×8 раскрашены в шахматном порядке. Одним ходом разрешается перекрасить любую клетку в цвет одной из соседних с ней клеток. Можно ли с помощью таких перекрашиваний изменить цвет всех клеток на противоположный? (Соседними считаются клетки, имеющие общую сторону)(4 балла)
- Один сплав состоит из двух металлов, входящих в него в отношении 2:3. Из скольких частей обоих сплавов можно получить новый сплав, содержащий те же металлы в отношении 17:27? (4 балла)
- Пусть в треугольнике АВС выполняется неравенство АС >ВС. Докажите, что для медианы CD треугольника АВС, выполняется условие: угол ACD меньше угла BCD. (5 баллов)
- Английская задача: Профессор математического факультета Мерль Уайт, профессор философии Лесли Блэк и секретарь деканата Джин Браун завтракали за одним столом.
- Разве не удивительно, - заметила девушка, – что наши фамилии Блэк, Браун и Уайт и что у одного из нас волосы черные, у другого каштановые, а у третьего - совсем белые?
-Действительно, забавно, - заметила особа с чёрными волосами. А вы обратили внимание, что ни у одного из нас цвет волос не соответствует фамилии?
-Точно, вы правы! – воскликнул (или воскликнула) профессор Уайт. Какого цвета волосы у профессора Блэка, если цвет волос у девушек не каштановый?
РS. по - английски «уайт» - белый, «блэк» - черный, «браун» - каштановый.(4 балла)
- Найдите наименьше число, которое делится на 77, а при делении на 74 дает в остатке 48. (4 балла)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2007/2008 учебный год.
8 класс.
- Найти трехзначное число по следующим данным:
а) число делится на 5;
б) если это число умножить на цифру его единиц, то результат будет больше суммы его цифр на 548. (3 балла)
-
Из двух равных трапеций сложить параллелограммы. Применить результат к выводу формулы площади трапеции. (3 балла)
- Найти все целые числа х, у, удовлетворяющие уравнению
ху = у + 2х. (4 балла)
- Доказать, что сумма расстояний всякой точки от вершин многоугольника больше его полупериметра. (4 балла)
- Доказать, что если число не делится на 7, то его куб, увеличенный или уменьшенный на 1, делится на 7. Установить, в каком случае надо куб числа увеличить, а в каком - уменьшить, чтобы деление нацело было возможным. (5 баллов)
|
|
|
Решу егэ 2014 - advice-me.ru |
|