|
Поделиться:
Олимпиада по математике. 11класс. 2010 - 2014уч.г.
Задача 1. Какой остаток при делении на 5 дает число
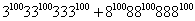 ? ?
Задача 2. Сколько корней имеет уравнение 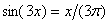 ? ?
Задача 3. Решите уравнение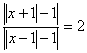 . .
Задача 4. При каких значениях параметра a функция 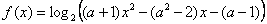 определена для всех x > 0? определена для всех x > 0?
Задача 5. В параллелограмме ABCD проведена средняя линия MN (M – середина AB, N – середина CD). Точка P делит отрезок BC в отношении 1:3 (считая от точки B), Q делит отрезок AD в отношении 2:3 (считая от точка А), O – пересечение PQ и MN. Найдите отношение MO к ON.
Задача 6. Какое наименьшее значение может принять выражение
cos(2x) – 2cos(x)?
Задача 7.
Вычислите

Задача 8. У Василия было много яблок, и он решил отдать их своим друзьям. Когда друзья пришли, он распределил яблоки между ними, причем всем досталось поровну. Неожиданно подошел еще один друг, яблоки пришлось перераспределить, и опять всем досталось поровну, но теперь на 15 штук меньше, чем в прошлый раз. Когда подошел еще один друг, яблоки снова перераспределили, опять всем досталось поровну, но в этот раз еще на 9 штуки меньше. Сколько яблок было у Василия и сколько в конце концов к нему пришло друзей?
Задача 9. Строительную компанию наняли построить дорогу из города N в город M, и за первый восьмичасовой рабочий день она построила 2 км дороги. Ночью прошел дождь и смыл всю разметку, которая была нарисована на построенном участке дороги. На следующий день разметка была восстановлена, и на это ушла часть рабочего времени. Скорость восстановления разметки – 6 км/ч. В результате на второй день был построен более короткий участок дороги. Следующей ночью вся разметка опять была смыта дождем, и ее восстановление снова потребовало части рабочего времени. На каком максимальном расстоянии могли находиться города N и М, если известно, что дорога между ними в результате была построена, и во время строительства каждую ночь шел дождь?
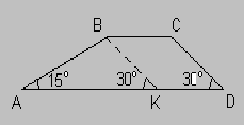
Задача 10. В трапеции ABCD длина основания AD равна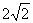 , а длина основания BC равна , а длина основания BC равна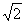 . Угол A = 15°, угол D = 30°. Найдите длину боковой стороны AB. . Угол A = 15°, угол D = 30°. Найдите длину боковой стороны AB.
Условие задачи изображено на рисунке:
Математическая олимпиада
11 класс
1.Решить уравнение: 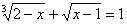
2.Может ли в правильной четырехугольной пирамиде площадь боковой грани быть больше, чем площадь диагонального сечения?
3.Найти целые решения системы:
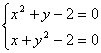
4. При каких значениях х и у многочлен 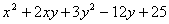 принимает наименьшее значение? принимает наименьшее значение?
5. Внутри угла в 600 взята точка, удаленная от сторон угла на 2см и на 11см. Найти расстояние от этой точки до вершины угла.
6.Доказать, что существует треугольник, высоты которого равны 3,4 и 5см. Какой это треугольник – прямоугольный, остроугольный или тупоугольный?
7. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют уравнению 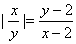 . .
8. Решить уравнение: 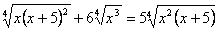 . .
9. Длины сторон прямоугольного треугольника составляют арифметическую прогрессию, а радиус вписанной в него окружности равен 4. Найти радиус описанной окружности.
10. Длина большей из двух диагоналей параллелограмма равна d, а один из углов, образованных диагоналями равен 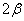 . Доказать, что периметр этого параллелограмма меньше, чем . Доказать, что периметр этого параллелограмма меньше, чем 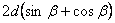 . .
11. Последовательность {an} задана условиями а1 =5; 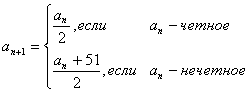 . .
12. Доказать, что если a >b >0, то 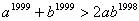 . .
13. Вершины А и В параллелограмма АВСD расположены по одну сторону от плоскости 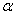 и удалены от этой плоскости на 5см и 3см соответственно. Найти расстояние от точки С до плоскости и удалены от этой плоскости на 5см и 3см соответственно. Найти расстояние от точки С до плоскости 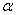 , если , если 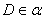 . .
14. Найти целые n>3, для которых n3-3 делится на n-3.
15. Решить уравнение: 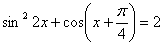 . .
16. СЕ – диаметр окружности описанной вокруг треугольника АВС, Н – точка пересечения высот треугольника. Доказать, что прямая ЕН проходит через середину стороны АВ.
17. Найти коэффициенты p и q квадратного трехчлена x2 +px+q, если известно, что остатки от деления на двучлен x-p и x-q соответственно равны p и q.
18. Решить иррациональное уравнение: 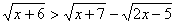 и в ответе указать наименьшее целое число, удовлетворяющее этому неравенству. и в ответе указать наименьшее целое число, удовлетворяющее этому неравенству.
19. Доказать, что две плоскости, проходящие через концы общих троек ребер куба, сходящихся в концах диагонали куба рассекает эту диагональ на три равные части.
20.Известно: сумма боковых сторон больше основания. Доказать, что она превышает основание меньше, чем удвоенный отрезок, соединяющий вершину с какой угодно точкой основания.
21. Вычислить значение суммы cos 4000 + cos 8000 + cos16000
22.Решить уравнение |x2-4| + |x2-1| = 3.
23. Сколько корней имеет квадратное уравнение x2 +px+q = 0, если известно, что p – q>1?
24. Цилиндр и конус имеют общее основание и пересекаются. Найдите объем их общей части, если объем каждого из них равен 27.
25. Докажите, что уравнение 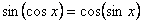 не имеет решений. не имеет решений.
26. Найти остаток от деления многочлена
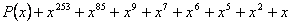 на х-1. на х-1.
27. Из квадратного листа жести со стороной a требуется вырезать развертку правильной четырехугольной пирамиды так, чтобы вершины квадрата склеивались в вершину пирамиды. Как это сделать, чтобы получить пирамиду наибольшего объема?
28. Решить систему: 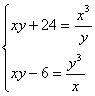
29. Около окружности описана трапеция, боковые стороны которой при продолжении пересекаются под углом 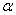 . Основания трапеции равны a и b (a>b) . Найти радиус окружности. . Основания трапеции равны a и b (a>b) . Найти радиус окружности.
30. Доказать, что при любых a и b справедливо неравенство: a2 + b2 +1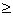 ab+ a+b. ab+ a+b.
31. Три квадрата расположены как на рисунке.
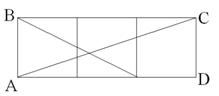
Найти величину угла между прямыми АС и ВD.
32. Решить уравнение:
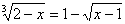
33. Построить график функции:
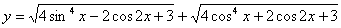 . .
34. Определить а так, чтобы сумма квадратов корней уравнения 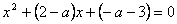 была была наименьшей. наименьшей.
Олимпиада 11 класс
Задача 1:
Для натурального n обозначим:
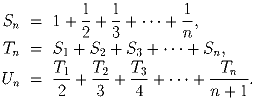
Найдите натуральные числа a,b,c,d, не большие 1000000, такие, что T1988 = aS1989 – b и U1988 = cS1989 – d.
Задача 2:
20 теннисистов устроили между собой соревнование из 14 игр. В каждой игре участвует 2 человека и каждый из этой компании теннисистов принял участие хотя бы в одной игре. Докажите, что в некоторых 6 играх участвовало 12 различных теннисистов.
Задача 3:
В остроугольном треугольнике ABC AB < AC < BC, I – центр вписанной окружности, O – центр описанной окружности. Докажите, что прямая IO пересекает стороны AB и BC.
Задача 4:
Номера лицензий, выдаваемых каждым штатом состоят из 6 цифр (кажда от 0 до 9). Каждые два номера должны отличаться не менее чем в двух цифрах. (Таким образом номера 027592 и 020592 не могут использоватьс одновременно.) Найдите максимальное количество лицензий, которые может выдать штат.
Задача 5:
Ожерелье A составлено из 14, а ожерелье B из 19 бусин. Докажите, что для любого нечетного n > 1 можно так перенумеровать все 33 бусины числами от n до n + 32, что номера любых двух соседних бусин будут взаимно просты. (Ожерелье здесь рассматривается как круг, на котором каждая бусина имеет двух соседей.)
Задачи математического боя . 11 класс.
1 Решите систему уравнений:
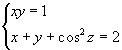
2. В четырехугольнике ABCD точка E — середина AB, F — середина CD. Доказать, что середины отрезков AF, BF, CE и DE являются вершинами параллелограмма.
3. Квадратная клетчатая таблица 3 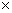 3 заполнена числами так, что суммы чисел во всех квадратах 2 3 заполнена числами так, что суммы чисел во всех квадратах 2 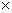 2 равны между собой. Доказать, что равны и суммы чисел на диагоналях. 2 равны между собой. Доказать, что равны и суммы чисел на диагоналях.
4. На каждой из планет сидит астроном, который наблюдает ближайшую. Доказать, что если число планет нечетно, то одну планету никто не наблюдает. Расстояния между планетами все различны.
5. Даны числа a0, a1, …, a2000, a2001. Известно, что все числа кроме крайних равны сумме соседних с ними чисел. Найти a2001, если известно, что a0 = 1.
6. Решить в целых числах уравнение x4 + 4y4 = 2(z4 + 4u4).
7. На плоскости дано несколько кругов, занимающих площадь 1. Доказать, что можно выбрать несколько непересекающихся кругов, площадь которых не меньше 1/9.
Математическая олимпиада
11 класс
Задача 1:
Каждый из 8 ящиков содержит 6 шаров. Каждый шар окрашивается в один из n цветов так, что ни в одном из ящиков нет шаров одного цвета и никакие два цвета не встречаются вместе более, чем в одном ящике. Найти наименьшее n, для которого это возможно.
Задача 2:
В треугольник ABC вписана окружность. Пусть D1 и E1 — точки касания окружности со сторонами BC и AC соответственно Пусть D2 и E2 — точки на сторонах BC и AC соответственно такие, что CD2 = BD1и CE2 = AE1. Пусть P есть точка пересечения AD2 и BE2. Окружность пересекает отрезок AD2 в двух точках. Обозначим через Q ту из них, которая ближе к A. Доказать, что AQ = PD2.
Задача 3:
Для неотрицательных вещественных чисел a,b,c, связанных равенством a2 + b2 + c2 + abc = 4, доказать неравенство 0< ab + bc + ca – abc < 2.
Задача 4:
В плоскости треугольника ABC взята точка P так, что PA,PB, и PC являются длинами сторон тупоугольного треугольника со стороной PA, противолежащей тупому углу. Доказать, что угол BAC острый.
Задача 5: Пусть S есть некоторое множество целых чисел (не обязательно положительных) такое, что
(A) существуют взаимно простые числа a и b в S, для которых a – 2 и b – 2 также являются взаимно простыми;
(B) если x и y — элементы из S (возможно, равные), то x2 – y также принадлежит S.
Доказать, что S есть множество всех целых чисел.
Задача 6:
Каждой точке плоскости сопоставлено вещественное число так, что выполнено следующее свойство: для всякого треугольника число, сопоставленное центру вписанной в него окружности, совпадает со средним арифметическим чисел, сопоставленных его вершинам. Доказать, что всем точкам плоскости сопоставлено одно и то же число
ПРИМЕРНЫЕ ЗАДАНИЯ
школьного этапа олимпиады по математике
2008-2009 учебный год.
11 класс.
1.Доказать, что сумма двух взаимно-обратных положительных чисел не меньше двух.
(2 балла)
2. Упростите 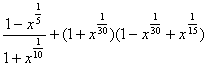 (2б) (2б)
3.Укажите значения аргумента, при которых функция
у = 2+ соs3х принимает наибольшее и наименьшее значения. Найдите эти значения функции. (4 балла)
4.Основания равнобедренной трапеции равны 3м и 8м, а угол при основании 600.
Найдите диагональ. (6 баллов)
5.Определите p, если сумма кубов корней уравнения 2x2-8х+p = 0 равна 34. (6 баллов)
Олимпиада
11 класс
1. Постройте эскиз графика функции:
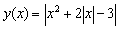 . .
Решение. Поскольку функция четная, достаточно описать ее для неотрицательных значений аргумента. Имеем: 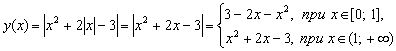 . .
Заметим, что вершина М параболы 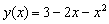 имеет координаты (-1;4). имеет координаты (-1;4).
2. При каких значениях числового параметра а неравенство 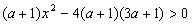 верно при всех значениях х? верно при всех значениях х?
Ответ. 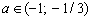 . .
Решение. При а=-1 имеем 0>0, что неверно.
При а>-1 сократим неравенство на (а+1), сохраняя знак:
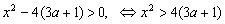 . .
Такое неравенство верно для всех х только
при 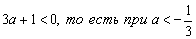 . .
При а<-1 сократим неравенство на (а+1), меняя знак на противоположный:
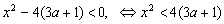 . .
Но квадрат числа никогда не бывает отрицательным.
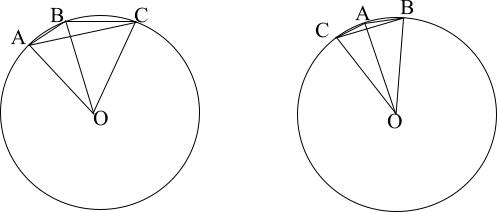
3. Треугольник со сторонами 4 см и 6 см вписан в окружность радиуса 12 см. Найдите длину третьей стороны треугольника.
Ответ. 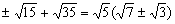
Решение.
Понятно, что искомый треугольник тупоугольный, и возможны два случая расположения его сторон АВ=4 см, ВС=6 см, как изображено на рисунках. Для решения задачи достаточно, например, найти косинус угла ВАС и применить теорему косинусов.
Имеем: ?ВАС = 0,5?ВОС как вписанный. А из равнобедренного треугольника ВСО со сторонами 6, 12, 12 см следует, что 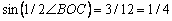 . Отсюда . Отсюда 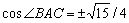 (по основному тригонометрическому тождеству). Пусть АС=х, запишем теорему косинусов: (по основному тригонометрическому тождеству). Пусть АС=х, запишем теорему косинусов:
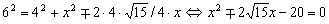
Один из корней каждого из уравнений отрицателен и не подходит. Положительные корни имеют величину: 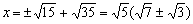 . .
4. По кругу сидят 2010 хамелеонов. Каждый из них может менять свой цвет в следующем порядке: синий, оранжевый, фиолетовый, зеленый, синий и т.д. Если прикоснуться к одному из хамелеонов, то он меняет свой цвет на следующий по порядку. При этом одновременно с ним меняют свой цвет трое хамелеонов, следующих за ним по часовой стрелке. Сначала все хамелеоны синие. Можно ли добиться того, чтобы все они стали зелеными?
Ответ. Этого добиться нельзя.
Решение. Поставим в соответствие каждому из цветов число: синему – 0; оранжевому – 1; фиолетовому – 2; зеленому – 3. Сначала хамелеоны все синие и сумма всех чисел равна 0, то есть кратна 4. При прикасании к какому-нибудь хамелеону сумма чисел увеличивается на 4. Без ограничения общности можно считать, что каждому из хамелеонов поставлен в соответствие один из возможных остатков от деления натуральных чисел на 4. Поэтому на каждом шаге такого процесса сохраняется делимость на 4. Однако сумма чисел 2010 зеленых хамелеонов равна 6030, и не кратна 4. Противоречие.
5. В каком году родились люди, которым в 2010 году исполнилось столько лет, какова сумма цифр их года рождения?
Ответ. 1986 или 2004.
Решение. Сумма цифр года рождения людей, родившихся в 19 веке, не превышает 28. Такие люди могут родиться только в 20-м или 21-м веке. Рассмотрим оба случая отдельно:
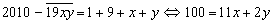 . .
Из уравнения следует, что х четная цифра и равна 8 (иначе не подобрать у), а у=6.
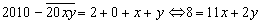 . .
Из уравнения следует, что х=0, у=4.
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2010/2011 учебный год.
11 класс.
- Обозначим две какие-нибудь цифры буквами А и Х. Докажите, что шестизначное число АХАХАХ делится на 7 без остатка. (3балла)
- Решите систему уравнений:
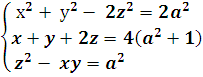 (3 балла) (3 балла)
- За круглым столом были приготовлены 12 мест для жюри с указанием имени на каждом месте. Николай Николаевич, пришедший первым, по рассеянности сел не на свое место, а на следующее по часовой стрелке место. Каждый член жюри, подходивший к столу после этого, занимал своё место или, если оно уже было занято, шел вокруг стола по часовой стрелке и садился на первое свободное место. Возникшее расположение членов жюри зависит от того, в каком порядке они подходили к столу. Сколько может возникнуть различных способов рассадки жюри?. (4 балла)
- Углы треугольника образуют арифметическую прогрессию, синусы удвадцатеренных углов, взятых в той же последовательности, также образуют арифметическую прогрессию. Найдите углы треугольника.
- Дана трапеция ABCD с основаниями AD =a и BC =b . Точки M и N лежат на сторонах AB и CD соответственно, причем отрезок MN параллелен основаниям трапеции. Диагональ АС пересекает этот отрезок в точке О. Найдите MN, если известно, что площади треугольников АМО и СNО равны? (5 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2009/2010 учебный год.
11 класс.
- Найдите остаток от деления многочлена
Р(х) = 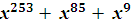 + +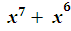 + + 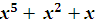 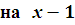 .(4 балла) .(4 балла)
- Решить систему уравнений:
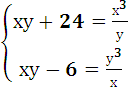 .(4 баллa) .(4 баллa)
>
- Из квадратного листа жести со стороной а требуется вырезать развертку правильной четырехугольной пирамиды так, чтобы вершины квадрата склеивались в вершину пирамиды. Как это сделать, чтобы получить пирамиду наибольшего объема? (5 баллов)
- Около окружности описана трапеция, боковые стороны которой при продолжении пересекаются под углом ?. Основания трапеции равны a и b (a > b). Найти радиус окружности. (5 баллов)
- Доказать, что при любых
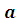 и и 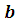 справедливо равенство: справедливо равенство:
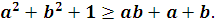
(6 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2008/2009 учебный год.
11 класс.
- Найдите все значения параметра а, при которых уравнение
(2 + а)x2- 2ах + 3а =0 имеет два положительных корня? (2 балла)
- Найдите наименьшее значение функции
у = х( х + 1)(х + 2)(х + 3) (4 балла)
- Трапеция разделена диагоналями на четыре части. Определите площадь трапеции по площадям частей, прилегающих к основанию. (4 балла)
- Найдите угол между противоположными ребрами тетраэдра.
(5 баллов)
- Решить систему уравнений:
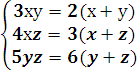 .(5 баллов) .(5 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2007/2008 учебный год.
11класс.
- Найти коэффициенты p и q квадратного трехчлена х2+ pх + q, если известно, что остатки от деления на двучлен х-p и х-q соответственно равны p и q . (3 балла)
- Решить иррациональное неравенство:
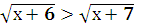 - -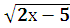 и в ответе указать наименьшее целое число, удовлетворяющее этому неравенству. (3 балла) и в ответе указать наименьшее целое число, удовлетворяющее этому неравенству. (3 балла)
- Доказать, что две плоскости, проходящие через концы общих троек ребер куба, сходящихся в концах диагонали куба, рассекает эту диагональ на три равные части. (4 балла)
- Найти целые решения системы: х2 + у-2=0 и х + у2-2=0
(5 баллов)
- Известно: сумма боковых сторон треугольника больше основания. Доказать, что она превышает основание меньше, чем на удвоенный отрезок, соединяющий вершину с какой угодно точкой основания.
(5 баллов)
|